Fibonacciho sekvencia – postupnosť v hudbe

Fibonacciho postupnosť je postupnosť čísiel, v ktorej každý ďalší člen F je súčtom dvoch predchádzajúcich. Fibonacciho postupnosť a Fibonacciho čísla nazval francúzsky matematik Édouard Lucas (1842-1891) podľa stredovekého talianskeho matematika Leonarda z Pisy, prezývaného Fibonacci. Postupnosť sa niekedy nazýva aj zlatá cesta (z gréc. χρνσοδρομος, chrysodromos).

Skúsme pokračovať sami aspoň po F10:

F6 = F4 + F5 = 3 + 5 = 8, postupnosť je (0, 1, 1, 2, 3, 5, 8)

F7 = F5 + F6 = 5 + 8 = 13, postupnosť je (0, 1, 1, 2, 3, 5, 8, 13)

F8 = F6 + F7 = 8 + 13 = 21, postupnosť je (0, 1, 1, 2, 3, 5, 8, 13, 21)

F9 = F7 + F8 = 13 + 21 = 34, postupnosť je (0, 1, 1, 2, 3, 5, 8, 13, 21, 34)

F10 = F8 + F9 = 21 +34 = 55, postupnosť je (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55)

*

Zlatý rez

Johannes Kepler upozornil na skutočnosť, že podiel dvoch po sebe nasledujúcich fibonacciho čísel ( F n + 1 F n ) {\displaystyle \left({\tfrac {F_{n+1}}{F_{n}}}\right)} konverguje k číslu, ktoré bolo známe už od antiky, označuje sa symbolom φ (grécke písmeno fí) a nazýva sa tiež zlatý rez. Vyjadrené modernou matematikou:

Súčet postupnosti

Fibonacciho čísla sa vyskytujú v sumách „plytkých“ uhlopriečok v Pascalovho trojuholníka (pozri koeficient dvojčlen). Fibonacci čísla možno nájsť v rôznych spôsoboch v poradí binárnych reťazcov.

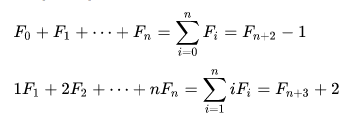
Výskyt Fibonacciho postupnosti v prírode je taký častý, že to nemožno pokladať za náhodu. Niekoľko príkladov:

Počet korunných lupienkov v kvetoch

  trojlist, šípová ruža, iskerník, nátržník, krvavček, krasuľka, ľalia, kosatec, fialka, astra, sedmokráska, stračonôžka, gailardia, …

         Často sa vyskytujúci počet korunných lupienkov:

3 –trojlist, ľalia, kosatec

5 – orlíček, stračonôžka, fialka

8 – krasuľka, iskerník, stračonôžka, krvavček

13 – chryzantémovka

21 – astra

34, 55, 84 – sedmokráska

Zoskupenie listov, výhonkov a vetvičiek

Označme si jeden list na stonke číslom 0 a na myslenej špirále spočítajme listy nad ním, až kým sa nedostaneme presne na úroveň listu 0 (predpokladáme, že nijaký nechýba). Počet listov i obrátok na špirále bude s veľkou pravdepodobnosťou Fibonacciho číslo. Pomer listov k obrátkam sa nazýva filotaxia (z gréc. usporiadanie listov) a býva spravidla jedným z Fibonacciho zlomkov (pomer dvoch susedných Fibonacciho čísel)

Počet pravotočivých a ľavotočivých špirál na borovicovej šiške (ide o susedné Fibonacciho čísla – niekedy sú to aj susedné Lucasove čísla, ktoré tvoria Lucasovu postupnosť. 1, 3, 4, 7, 11, 18, …Platí pre ňu pravidlo fibonacciovskej postupnosti: každé číslo (počnúc tretím) je súčtom predchádzajúcich dvoch. Lucasova postupnosť je pomenovaná podľa Edurda Lucasa, matematika 19. storočia, ktorý študoval rekurentné a dal meno Fibonacciho postupnosti. Medzi týmito dvoma postupnosťami exsistuje následovný vzťah:

*

Fibonacciho sekvencia – postupnosť v hudbe – video

7 -11 sekunda / tak, ako je uvedená v stupnici
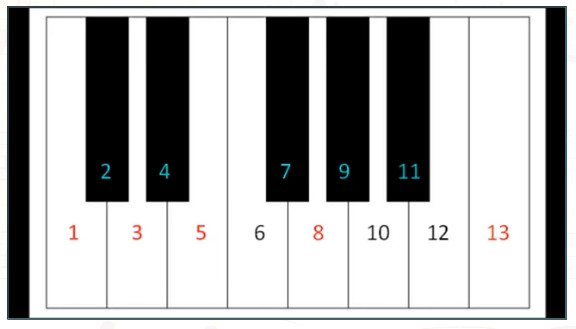
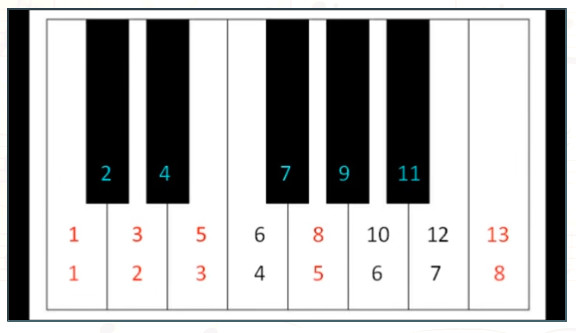
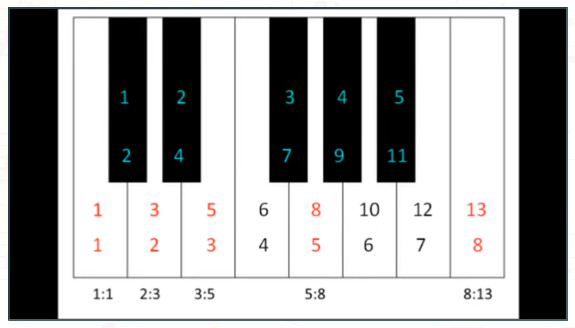
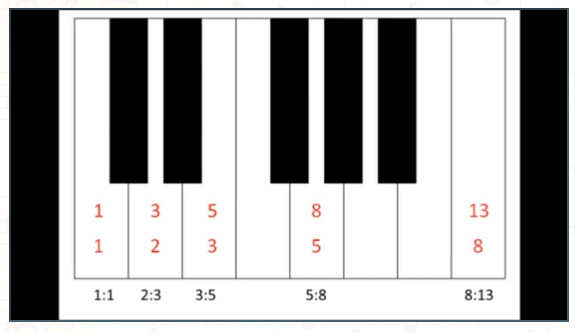
12 – 16 sekunda / ilustrované na klavíri na adrese www.astrosound.org
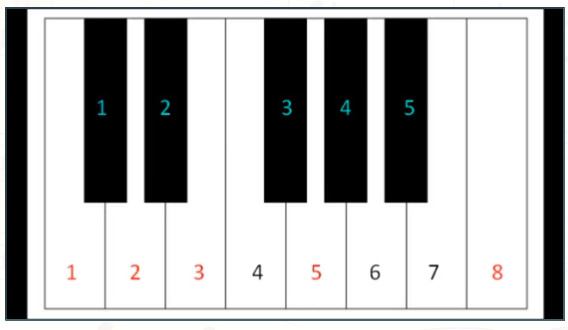
23 – 27 sekunda / 8 bielych klávesov k 5 čiernym klávesom
50 – 56 sekunda / 5: 8
57 – 56 sekunda / 8 bielych klávesov z celkove 13-tich klávesov
1:18 – 56 sekunda / 8:13

*

———————————————————————————————-

*

V jednej oktáve sa nachádza 13 poltónov (klávesov)  / 13

*

*

V jednej oktáve sa nachádza 8 bielych a 5 čiernych klávesov / 5 : 8

*

1 oktáva = C – Cis – D – Dis – E – F – Fis – G – Gis – A – Ais – H – c (použíté krížiky“♯„)

*

1 oktáva = C – Des – D – Es – E – F – Ges – G – As – A – B – H – c /pričom B = Hb/ (použíté béčka „b“)

*

8 bielych klávesov (c – d – e – f – g – a – h – c1) / 8

*

5 čiernych klávesov (cis – dis – fis – gis – ais) alebo (des – es – ges – as – b) / 5

*

Všetkých klávesov do oktávy je 13, z toho bielych je 8 / 13 : 8

*

Všetkých klávesov do oktávy je 13, z toho bielych je 8 a čiernych 5 / 5, 8, 13

*

Horná rada čísiel = fibonacciho postupnosť (súčet), dolná rada číslovanie bielych klávesov

*

https://sk.wikipedia.org/wiki/Fibonacciho_postupnos%C5%A5

https://fibonaccihopostupnost.estranky.sk/clanky/postupnost-v-prirode/

*